Una fuerza representa la acción de un
cuerpo sobre otro y se caracteriza por su punto de aplicación, magnitud o
módulo y dirección. Pero las fuerzas sobre una partícula tienen el mismo punto
de aplicación. Por tanto, cada fuerza considerada estará definida por su
magnitud y dirección.
La fuerza en sí se representa por un
segmento de esa línea, mediante el uso de una escala apropiada, puede escogerse
la longitud de este segmento para representar la magnitud de la fuerza.
Finalmente el sentido de la fuerza debe indicarse por una punta de flecha. En
la definición de una fuerza es importante indicar su sentido. Dos fuerzas como
las mostradas en la siguiente figura, tienen la misma magnitud y la misma línea
de acción pero diferente sentido, tendrán efectos opuestos sobre una partícula.
La evidencia experimental muestra que dos
fuerzas P y Q que actúan sobre una partícula A pueden sustituirse por una sola
fuerza R que produce el mismo efecto sobre la partícula. A esta fuerza se le
llama resultante de las fuerzas P y Q y puede obtenerse al construir un
paralelogramo con P y Q como lados. La diagonal que pasa por A representa la
resultante. Esto se conoce como la Ley del paralelogramo para la adición de dos
fuerzas, y se basa en la evidencia experimental, no puede probarse ni derivarse
de manera matemática.
VECTORES
En apariencia las fuerzas no obedecen
reglas de la adición definidas en la aritmética o en el álgebra ordinaria. Por
ejemplo, dos fuerzas que actúan formando un ángulo recto, una de 4 Lb y otra de
3 Lb, suman una fuerza de 5 Lb y no una de 7 Lb. Las fuerzas no son las únicas
cantidades que siguen la ley del paralelogramo para la adición.
Los vectores se definen como expresiones
matemáticas que poseen magnitud, dirección y sentido, los cuales se suman de
acuerdo con la ley del paralelogramo.
ADICION O SUMA DE VECTORES
La suma de dos vectores P y Q se obtiene
uniendo los dos vectores al mismo punto A y construyendo un paralelogramo que
tenga por lados a P y a Q. La diagonal que pasa por A representa la suma
vectorial de P y Q, y se representa por P+Q.
PROBLEMAS
PROBLEMA RESUELTO 4.5
Un peso de
400 lb se une a la palanca mostrada en la figura en el punto A. La constante
del resorte BC es K=250 lb/in y este no se encuentra deformado
cuando
Θ=0. Determine la posición de equilibrio.
DIAGRAMA DE CUERPO LIBRE.
Se dibuja el diagrama de cuerpo libre
de la palanca junto al cilindro. Represente con s la elongación del resorte a
partir de la posición en que este no se encuentra deformado y observe que s=rΘ, se tiene que F=ks=krΘ.
ECUACION DE EQUILIBRIO. Sumando los momentos de W y de F con respecto a O, se escribe:
Sustituyendo los datos
numéricos que fueron proporcionados se obtiene:
Al resolver
numéricamente, se encuentra que
Θ= 0 Θ=80.3°
Problema 2
El marco
mostrado en la figura sostiene una parte del techo de un pequeño edificio. Se
sabe que la tensión en el cable es de 150 KN, determine la reacción en el
extremo fijo E.
Solución
Diagrama de cuerpo
libre. Se dibuja el
diagrama de cuerpo libre del marco junto con el cable BDF. La reacción en el
extremo fijo E está representada con los componentes de la fuerza Ex
y Ey y por el par ME. las otras fuerzas actúan sobre el
diagrama de cuerpo libre son las cuatro cargas de 20 KN y la fuerza de 150 KN
ejercida en el extremo F del cable.
(20 KN) (7.2 M)+ (20
KN) (5.4 M)+ (20 KN) (3.6 M)+(20 KN) (1.8 M)- 6/7.5(150 KN) (4.5 M)+ ME=0
ME=180.0
KN.M
ME=180 KN. M
Problema 3
Se aplican tres cargas a una viga como
se muestra en la figura. La viga se apoya en un rodillo en A y en un perno en
B. Sin tomar en cuenta el peso de la viga, determine las reacciones en A y B
cuando P=15 kips
Diagrama de cuerpo libre. Se dibuja un diagrama de cuerpo
libre de la viga. La reacción en A es vertical y se representa con A. La
reacción en B se representa con las componentes Bx y By.
Se supone que cada componente actúa en la dirección mostrada e la figura.
Ecuaciones de equilibrio. Se escriben las tres ecuaciones de
equilibrio siguientes y se resuelven para las reacciones señaladas.
-(15 kips)(3
ft) + By(9 ft) – (6 kips)(11 ft)-(6 kips)(13 ft) = 0
By=
21.0 kips
By=21.0
kips ↑
-A (9 ft) + (15 kips)
(6 ft) – (6 kips) (2 ft) – (6 kips) (4 ft)=0
A=6 kips
A= 6 kips ↑
Comprobación. Se comprueban los resultados sumando
las componentes verticales de todas las fuerzas externas.
6 kips – 15 kips + 21
kips – 6 kips – 6 kips=0
Capítulo
3
CUERPOS RIGIDOS: SISTEMAS EQUIVALENTES DE FUERZA
3.1 FUERZAS EXTERNAS E INTERNAS.
Las fuerzas que actúan sobre los cuerpos rígidos se
pueden dividir en dos grupos: 1) fuerzas externas y 2) fuerzas internas.
1. Las fuerzas externas
representan la acción que ejercen otros cuerpos sobre el cuerpo rígido en
consideración. Ellas son las responsables del comportamiento externo del cuerpo
rígido. Las fuerzas externas causan que el cuerpo se mueva o aseguran que éste
permanezca en reposo.
2. Las fuerzas internas son
aquellas que mantienen unidas las partículas que conforman al cuerpo rígido. Si
éste está constituido en su estructura por varias partes, las fuerzas que
mantienen unidas a dichas partes también se definen como fuerzas internas.
Como
ejemplo de fuerzas externas, consideren se las fuerzas que actúan sobre un
camión descompuesto que es arrastrado hacia delante por varios hombres mediante
cuerdas unidas a la defensa delantera (figura 3.1). Las fuerzas externas que
actúan sobre el camión se muestran en un diagrama de cuerpo libre (fıgura 3.2).
En primer lugar, se debe considerar el peso del camión. A pesar de que el peso
representa el efecto de la atracción de la Tierra sobre cada una de las
partículas que constituyen al camión, éste se puede representar por medio de
una sola fuerza W. El punto de aplicación de esta fuerza, esto es, el punto en
el que actúa la fuerza, se defıne como el centro de gravedad del camión.
3.3. PRINCIPIO DE TRANSMISIBILIDAD. FUERZAS EQUIVALENTES.
El principio de transmisibilidad establece que las condiciones de
equilibrio o de movimiento de un cuerpo rígido permanecerán inalteradas si una
fuerza F que actúa en
un punto dado de ese cuerpo se reemplaza por una fuerza F’ que tiene la
misma magnitud y dirección, pero que actúa en un punto distinto, siempre
y cuando las dos fuerzas tengan la misma línea de acción.
Las dos fuerzas, F y F’,
tienen el mismo efecto sobre el cuerpo rígido y se dice que son equivalentes.
Es te principio estable ce que la acción de una fuerza puede ser transmitida a lo largo de su línea de
acción.
3.6 MOMENTO DE UNA FUERZA CON RESPECTO A UN PUNTO.
Considere
a F como una fuerza que es aplicada en
un cuerpo rígido. El efecto que tendrá la fuerza sobre el cuerpo rígido
dependerá de donde apliquemos dicha fuerza. Del punto O a A se le conoce como
vector de posición (r).
El
momento de la fuerza con respecto al punto O queda definido como el producto
vectorial de r y F:
Mo=
r x F
El
momento siempre será perpendicular al
plano donde se ubique el punto de referencia, en este caso O. El momento
será positivo de acuerdo a su giro.
Por
último si contamos con α que es el ángulo formado por las líneas de acción del
vector r y la fuerza F, podemos calcular el momento de la siguiente manera:
Mo=r
F senα= Fd
Las
unidades en las que estára dado el momento será newton-metro.
3.8. COMPONENTES RECTANGULARES DEL MOMENTO DE UNA FUERZA
En
general, la deteminación del momento de una fuerza en el espacio se simplifica
en forma considerable si el vector de fuerza y el vector de posición a partir
de su punto de aplicación se descomponen en sus componentes rectangulares x ,y
y z . Considere el momento M0 con respecto a O de una fuerza F con componentes
Fx, Fy y Fz que está aplicada en el punto A de coordenadas x ,y y z. Se observa
que las componentes del vector de posición r son iguales, respectivamente, a
las coordenadas x ,y y z del punto A.
Al
sustituir a r y a F y recordar los resultados obtenidos, se puede escribir el
momento M0 de F con respecto a O de la siguiente forma
Donde las componentes escalares Mx, My y M. están definidas por las relaciones
También
puede escribirse a Mo en forma de determinante










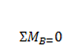






muy bueno bro sigue adelante !!
ResponderEliminar